Kurzstrecken mit dem Auto
Es ist erstaunlich welche Wege wir zu Fuß oder mit dem Fahrrad zurücklegen können. Oder sollte ich sagen könnten oder sogar sollten?
Problem
Ich habe mir von kompetenter Seite sagen lassen, dass Kurzstrecken mit dem Auto unter anderem für das Fahrzeug selbst nicht gut, sondern eher schädlich sind. Der Motor erreicht nicht die optimale Betriebstemperatur und wird daher nicht gut geschmiert. Durch die niedrige Temperatur wird auch mehr Treibstoff benötigt, da das Verbrennungsgemisch "fetter" sein muss. Das heißt, auch der Geldbeutel wird stärker belastet.
Zusätzlich belasten solche kurzen Fahrten auch die Luft und sind der eigene Gesundheit nicht zuträglich.
Wie kann ich also daran erinnert werden Kurzstrecken mit dem Auto zu vermeiden? Und was sind Kurzstrecken hier überhaupt?
Kurzstrecke
Für ein Auto sind Kurzstrecken sicher in wenigen Kilometern anzugeben, wenn ich allerdings als Alternative meine Füße oder mein Fahrrad habe, muss ich das genauer definieren. Ich persönlich finde fünf Kilometer Radfahren noch nicht weit, kann aber gut nachvollziehen, dass das nicht jedem so geht. Zwei Kilometer sind aber sicher kurz. Fünf mal um den Sportplatz ist mit dem Fahrrad zu schaffen, daher definiere ich hier eine
Kurzstrecke als Entfernung zwischen Start und Ziel von höchstens zwei Kilometer Länge.
Idee
Wie kann man also daran erinnert werden, diese Fahrten zu vermeiden und eventuell per Fahrrad oder zu Fuß zurückzulegen und so
-
das Auto und
-
den Geldbeutel zu schonen,
-
nebenbei ein bisschen für die eigene Gesundheit zu tun und
-
die Luft zu verbessern?
Also gleich vier gute Dinge gleichzeitig zu tun.
Die Automobilhersteller könnten die Autos so umbauen, dass man bevor man den Motor anmachen kann, das Fahrziel ins Navi eingeben muss. Das Navi berechnet zuverlässig den Weg und sagt einem wie weit die Strecke ist. Für das Auto und für das Fahrrad und für den Fußweg. Ist die Strecke zwei Kilometer oder kürzer berechnet der Bordcomputer einen angemessenen Preis für die Autofahrt. Dieser wird vom Fahrer bestätigt und sofort vom Konto des Fahrers abgebucht, wenn mit dem Auto gefahren werden soll. Ist die Transaktion abgeschlossen kann das Auto gestartet werden und los geht’s. Falls der Preis nicht bestätigt wird, muss ein anderes Transportmittel oder ein anderes Ziel gewählt werden.
Der angemessene Preis
Der Preis muss so gewählt sein, dass die Entscheidung das Auto zu schonen leicht fällt. Er muss natürlich auch dem Auto angepasst sein und bei steigender Kilometerzahl abnehmen. Das lässt sich leicht mit einer Funktion in Abhängigkeit von der Länge der Fahrtstrecke und dem individuellen Kilometerpreis für das Auto modellieren.
Ich modelliere nur den Faktor für den Aufschlag für die Kurzstrecke und da sich im Leben auch kaum etwas abrupt ändert, wähle ich eine Funktion \$a(x)\$, die auch ab dem 2001-ten Meter noch ein bisschen Aufschlag berechnet und ab 3000 Metern, also sieben einhalb Platzrunden, und mehr so gut wie keinen Aufschlag mehr ausgibt. Den Faktor muss man dann noch mit dem individuellen Kilometerpreis multiplizieren und erhält den individuellen Aufschlag für sein Auto. Also habe ich für den Faktor:
-
\$a(0) = 100\$, das hundertfache des Kilometerpreises für nur Motor an und gar nicht fahren.
-
\$a(2) = 50\$, das fünfzigfache des Kilometerpreises für zwei Kilometer fahren.
-
\$a(3) = \frac{1}{100}\$, ein Aufschlag von einen hundertstel des Kilometerpreises für drei Kilometer fahren, und dann
-
\$lim_{x->\infty} a(x) = 0\$, kein spürbarer Aufschlag mehr. Der Wert wird so klein, dass eine Rundung auf Eurocent 0 liefert!
Mit einem bisschen Rechnen bin ich für meine Faktorfunktion auf diese Lösung gekommen:
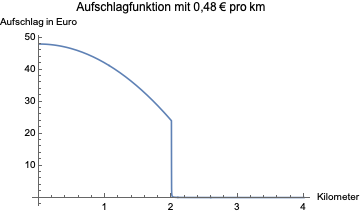
Setzt man jetzt die Länge der zu fahrenden Strecke in Kilometer ein und multipliziert den Wert mit dem individuelle Kilometerpreis für das eigene Auto ergibt sich der Aufpreis für’s Autofahren. So sieht das für einen Kilometerpreis von 0,48€ für die ersten vier Kilometer aus:
| Kilometer | Aufschlag in Euro | Grafik |
|---|---|---|
0,0 |
48,00 |
|
0,5 |
46,50 |
|
1,0 |
42,00 |
|
1,5 |
34,50 |
|
2,0 |
24,00 |
|
2,5 |
0,01 |
|
3,0 |
0,00 |
|
3,5 |
0,00 |
|
4,0 |
0,00 |
FAZIT
Die Fahrt zum Bäcker und zurück kostet jetzt 48,00€, plus die 1,92€ Kilometerpreis natürlich, und dass lässt mich schon überlegen, ob ich nicht anders an meine Brötchen komme. Per Rad zum Beispiel, oder gar zu Fuß. Es böte sich auch an eine Fahrgemeinschaft zu gründen, so dass man sich die Kosten durch, sagen wir fünf, teilte. Dann wäre das Kfz. auch mit Passagieren ausgelastet. (Apropos Auslastung, dazu habe ich hier etwas geschrieben)
Grundsätzlich bleibt festzuhalten, dass eine Kurzstrecke dem Auto nicht gut tut. Das eine wirksame Erinnerung vor jeder Fahrt technisch keine allzu große Herausforderung ist. Die oben dargestellte aber vermutlich nicht so schnell durch die Automobilindustrie umgesetzt wird, da diese ja gerne Autos verkauft und geschonte Autos länger halten.
Es gibt aber Alternativen sich vor ungewollten Schäden am Auto durch häufige Nutzung auf Kurzstrecken zu schützen. Hier sind ein paar aufgeführt:
-
Das Auto ganz hinten in der Garage parken, davor alles Sport- und Freizeitgerät lagern und dann die Fahrräder leicht und einfach erreichbar parken.
-
Immer die Autoschlüssel im Tresor mit der 74-stelligen Pin ablegen.
-
Das Auto einfach immer vorm Bäcker parken.
-
Das Auto verkaufen und Car-Sharing nutzen.
-
Einen Bäcker mit Brötchenservice wählen.
Ich habe sehr lange die Garagenvariante gewählt und dann vor ca. 8 Jahren auf die Car-Sharing-Variante gewechselt. Nicht nur zum Brötchen kaufen, sondern auch für den Wocheneinkauf nutze ich mein Fahrrad und einen ordentlichen Anhänger. Ich kann das aus eigener Erfahrung empfehlen und wünsche Euch viel Spaß beim Kurzstrecken-Mit-Dem-Auto vermeiden!
Anhang
In diesem Anhang zeige ich, wie ich meine Aufschlagsfunktion modelliert habe. Es sind aus meiner Sicht leicht einsehbare mathematische Überlegungen, die eher dazu dienen meine Kenntnisse im Formelsatz auf Webseiten zu verbessern, als wirklich das Thema zu unterstreichen. Dennoch möchte ich Euch natürlich meine Überlegungen nicht vorenthalten. Also bitte schön.
Herleitung
Zur Erinnerung: Ich hatte folgendes für meine Funktion gefordert:
-
\$a(0) = 100\$, das hundertfache des Kilometerpreises für nur Motor an und gar nicht fahren.
-
\$a(2) = 50\$, das fünfzigfache des Kilometerpreises für zwei Kilometer fahren.
-
\$a(3) = \frac{1}{100}\$, ein Aufschlag von einen hundertstel des Kilometerpreises für drei Kilometer fahren, und dann
-
\$lim_{x->\infty} a(x) = 0\$, kein spürbarer Aufschlag mehr. Der Wert wird so klein, dass eine Rundung auf Eurocent 0 liefert!
Für die Punkte 1 und 2 lässt sich das leicht und gut genug mit einer Parabel \$p\$ annähern, also hat die Funktion für den Faktor hier folgende Form:
\$p(x) = a x^2 + b x + c\$
für die Punkte 3 und 4 ist eine Hyperbel \$h\$ eine gute und einfache Annäherung und damit die folgende Form:
\$h(x) = \frac{1}{d x + e}\$
Zusammengebaut ergibt sich für meine Faktorfunktion \$a\$:
Die Parabel
Aus den obigen Betrachtungen und dem Wunsch, dass die Parabel ihren Scheitelpunkt in 0 haben soll, ergeben sich für die Parabel folgenden Anforderungen:
-
\$p(0) = a \cdot 0^2 + b \cdot 0 + c = 100 \$
-
\$p(2) = a \cdot 2^2 + b \cdot 2 + c = 50 \$
-
\$p'(0) = 2a \cdot 0 + b = 0 \$
Aus 1. ergibt sich sofort: \$c=100\$. Aus 3. folgt genauso einfach: \$b=0\$ und ich kann \$a\$ einfach mit 2. ausrechnen:
Und damit gilt:
\$p(x) = -12.5 x^2 + 100\$
Die Hyperbel
Aus den obigen Betrachtungen und dem Wunsch, dass die Hyperbel in 2 die Parabel stetig fortsetzt, ergeben sich für die Hyperbel folgende Anforderungen:
-
\$h(2) = \frac{1}{d 2 + e} = 50 \$
-
\$h(3) = \frac{1}{d 3 + e} = \frac{1}{100} \$
Wenn ich 1. nach \$e\$ auflöse ergibt sich: \$e = \frac{1}{50} - 2 d \$. Das eingesetzt in 2. ergibt sich:
Und also \$e = \frac{1}{50} - 2 \cdot 99.98 = -\frac{9997}{59} = -199.94\$
Und damit gilt:
\$h(x) = \frac{1}{99.98 x - 199.94}\$